Given ↓
- The equation of the line 2x - 3y -5 = 0
To find ↓
- The slope of the line perpendicular to this line
Calculations ↓
First of all, we need to add 5 on both sides :
2x-3y=5
Now, subtract 2x on both sides ↓
-3y=5-2x
Or
-3y=-2x+5
Now we need to divide by -3 on both sides to get y all by itself ↓
y=-2/-3+5/-3
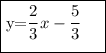
Now determining the slope is facile.
If lines are perpendicular to each other, they
- Intersect at a 90º angle
- Have slopes that are opposite reciprocals
In order to find the opposite reciprocal of a fraction, we need to switch the numerator & the denominator places and then change the fraction's sign as follows ↓
(slope = 2/3)
Switch the numerator and denominator places ↓
3/2
Change the fraction's sign ↓
-3/2
Therefore the slope's -3/2
hope helpful ~