Question

Find the geometric means in the following sequence. –14, ? , ? , ? , ? , –235,298

Answer 1

-98,-686,-4802,-33614

Explanation:

Answer 2

The geometric mean of the sequence is 1814.99.

Explanation:

The formula to compute the geometric mean is:

`GM=\sqrt[n]{a_(1)\cdot a_(2)\cdot a_(3)\cdot...a_(n)}`

The geometric sequence is:

–14, ? , ? , ? , ? , –235,298

The nth term of a geometric sequence is:

`a_(n)=a_(1)\cdot r^(n-1)`

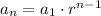
Here, r is the common ratio.

There are 6 terms in the sequence provided.

Compute the common ratio as follows:

`a_(6)=a_(1)\cdot r^(6-1)\\\\-235298=-14* r^(5)\\\\r=[(235298)/(14)]^(1/5)\\\\r=7`

Thus, the common ratio is 7.

The missing terms are:

`a_(2)=a_(1)\cdot r^(2-1)\\=-14* 7\\=-98`

`a_(3)=a_(1)\cdot r^(3-1)\\=-14* 7^(2)\\=-686`

`a_(4)=a_(1)\cdot r^(4-1)\\=-14* 7^(3)\\=-4802`

`a_(5)=a_(1)\cdot r^(5-1)\\=-14* 7^(4)\\=-33,614`

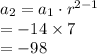
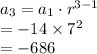
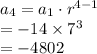
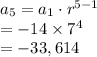
Compute the geometric mean as follows:

`GM=\sqrt[n]{a_(1)\cdot a_(2)\cdot a_(3)\cdot...a_(n)}`

`=\sqrt[6]{-14* -98* -686* -4802*-33614* -235298} \\\\=1814.9854\\\\\approx 1814.99`

Thus, the geometric mean of the sequence is 1814.99.