Question

asked Dec 5, 2021 185k views

1 Answer

Chris Satchell · Answer 1 · 2021-12-11T17:37:30+0000

Answer:

15.24% probability that at least 2 will still stand after 35 years

Explanation:

To solve this question, we need to understand the binomial distribution and the exponential distribution.

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)

In which
C_(n,x) is the number of different combinations of x objects from a set of n elements, given by the following formula.

C_(n,x) = (n!)/(x!(n-x)!)

And p is the probability of X happening.

Exponential distribution:

The exponential probability distribution, with mean m, is described by the following equation:

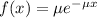
$f(x) = \mu e^(-\mu x)$

In which
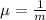$\mu = (1)/(m)$ is the decay parameter.

The probability that x is lower or equal to a is given by:

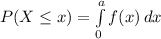
$P(X \leq x) = \int\limits^a_0 {f(x)} \, dx$

Which has the following solution:

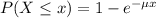
$P(X \leq x) = 1 - e^(-\mu x)$

The probability of finding a value higher than x is:

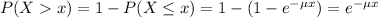
$P(X > x) = 1 - P(X \leq x) = 1 - (1 - e^(-\mu x)) = e^(-\mu x)$

Probability of a single tower being standing after 35 years:

Single tower, so exponential.

Mean of 25 years, so
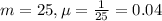
$m = 25, \mu = (1)/(25) = 0.04$

We have to find
P(X > 35)

$P(X > 35) = 1 - P(X \leq x) = 1 - (1 - e^(-\mu x)) = e^(-0.04*35) = 0.2466$

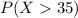
What is the probability that at least 2 will still stand after 35 years?

Now binomial.

Each tower has a 0.2466 probability of being standing after 35 years, so
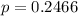
p = 0.2466

3 towers, so
n = 3

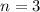
We have to find:

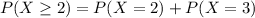
$P(X \geq 2) = P(X = 2) + P(X = 3)$

In which

P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)

P(X = 2) = C_(3,2).(0.2466)^(2).(0.7534)^(1) = 0.1374

P(X = 3) = C_(3,3).(0.2466)^(3).(0.7534)^(0) = 0.0150

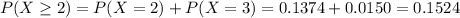
$P(X \geq 2) = P(X = 2) + P(X = 3) = 0.1374 + 0.0150 = 0.1524$

15.24% probability that at least 2 will still stand after 35 years

Please log in or register to add a comment.