Answer:
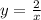
Step-by-step explanation:
Let's check all the answers to be sure we are correct!
Choice A) y = 2x
The domain for y = 2x is represented by the interval (-∞,∞). This shows that the domain is all real numbers.
Choice B) y = 2 + x
The domain is represented by the interval (-∞,∞). This shows that the domain is all real numbers.
Choice C)

We know that the denominator can not be equal to zero. You must remember this! So, now we find that the domain is represented by the interval,
(-∞,0) ∩ (0,∞)
This shows that the domain is all real numbers except the number zero.
Choice D)
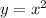
The domain is represented by the interval (-∞,∞). This shows that the domain contains all real numbers.
Therefore, our answer is choice C!
Nice job everyone!