Question

Which equation describes a relationship such that x = 0 must be excluded from the domain?

y = 2 x
y = 2 + x
y = 2/x
y = x ^2

Answer 1

`y = (2)/(x\\)`

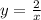
Step-by-step explanation:

Let's check all the answers to be sure we are correct!

Choice A) y = 2x

The domain for y = 2x is represented by the interval (-∞,∞). This shows that the domain is all real numbers.

Choice B) y = 2 + x

The domain is represented by the interval (-∞,∞). This shows that the domain is all real numbers.

Choice C)
`y=(2)/(x)`

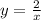
We know that the denominator can not be equal to zero. You must remember this! So, now we find that the domain is represented by the interval,

(-∞,0) ∩ (0,∞)

This shows that the domain is all real numbers except the number zero.

Choice D)
`y = x^(2)`

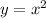
The domain is represented by the interval (-∞,∞). This shows that the domain contains all real numbers.

Therefore, our answer is choice C!

Nice job everyone!

Answer 2

y = 2/x

Step-by-step explanation:

You cannot divide by zero because you will get an undefined value, and this will create a hole in the graph.