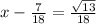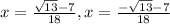Question

Use the quadratic formula to solve the equation​. 9x2−7x+1=0 Enter your answers, in simplified radical form. x = x =

Answer 1

`x=(√(13)-7 )/(18) ,x=(-√(13)-7 )/(18)`

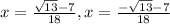
Explanation:

I'm not too good with the quadratic formula so I'm going to complete the square.

First divide everything by 9 and move the 1 to the other side.

`x^2-(7)/(9)=-(1)/(9)`

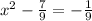
Then take half of
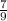`(7)/(9)` and square it and add it to both sides.

`x^2-(7)/(9) +(49)/(324)=(13)/(324)`

Now you can factor it.

`(x-(7)/(18))^2=(13)/(324)`

Square root:

`x-(7)/(18)=(√(13) )/(18)`

`x=(√(13)-7 )/(18) ,x=(-√(13)-7 )/(18)`