Answer:
The following graph represents the function g(x)=|x+4| +2
1) On a coordinate plane, an absolute value graph has a vertex at (-4,2)
Explanation:
A vertex can bed defined as a point where two lines meet. In a graph, a vertex can also be interpreted as the point where the direction of the line or curve change
The function is given by:
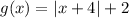
which is an absolute value function. We need to find the vertex of the graph.
The graph drawn is attached below.
We can see in the graph that at x = -4 and y = 2 , a point is formed where the straight line changes its direction.
So the vertex is formed at (-4,2)