Question

Suppose f(x) is continuous on [3,6] and −3≤f′(x)≤5 for all x in (3,6). Use the Mean Value Theorem to estimate f(6)−f(3).

Answer 1

Answer: -9 ≤ f(6) - f(3) ≤ 15

Explanation:

In order to use the Mean Value Theorem, it must be continuous and differentiable. Both of these conditions are satisfied so we can continue.

Find f(6) - f(3) using the following formula:

`f'(c)=(f(b)-f(a))/(b-a)`

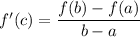
Consider: a = 3, b = 6

`\text{Then}\ f'(c)=(f(6)-f(3))/(6-3)\\\\\\\rightarrow \quad 3f'(c)=f(6) - f(3)`

Given: -3 ≤ f'(x) ≤ 5

-9 ≤ 3f'(c) ≤ 15 Multiplied each side by 3

→ -9 ≤ f(6) - f(3) ≤ 15 Substituted 3f'(c) with f(6) - f(3)