Answer:
Option D.
Explanation:
Statement given,
f(x) + 2 =

Or f(x) =
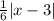 -2
-2
Parent function, g(x) = |x|
Absolute value function g(x) when shifted 3 units right,
g'(x) = |x - 3|
Vertically compressed by
 units and shifted 2 units down, then the new function will be
units and shifted 2 units down, then the new function will be
f(x) =
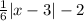
Characteristics of the graph of this function:
1). Vertex at (3, -2).
2). Vertical compression of the parent function by
 .
.
3). Graph opens upwards.
4). Range of the graph f(x) is f(x) ≥ -2.
Therefore, Option D will be the answer.