Question

The blood platelet counts of a group of women have a​ bell-shaped distribution with a mean of 258.7 and a standard deviation of 63.5. ​(All units are 1000 ​cells/mu​L.) Using the empirical​ rule, find each approximate percentage below. a. What is the approximate percentage of women with platelet counts within 3 standard deviations of the​ mean, or between 68.2 and 449.2​? b. What is the approximate percentage of women with platelet counts between 195.2 and 322.2​?

Answer 1

a)
`P( \mu -3\sigma <X< \mu +3\sigma)`

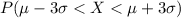
And from the empirical rule we know that this probability is 0.997 or 99.7%

b)
`P(195.2 <X<322.2)`

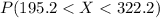
Using the z score we have:

`z = (322.2 -258.7)/(63.5)= 1`

`z = (195.2 -258.7)/(63.5)= -1`

And within one deviation from the mean we have 68% of the values

Explanation:

For this case we defien the random variable of interest X as "blood platelet counts" and we know the following parameters:

`\mu = 258.7, \sigma =63.5`

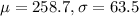
Part a

We can use the z score formula given by:

`z =(\bar X -\mu)/(\sigma)`

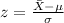
And we want this probability:

`P( \mu -3\sigma <X< \mu +3\sigma)`

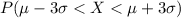
And from the empirical rule we know that this probability is 0.997 or 99.7%

Part b

For this case we want this probability:

`P(195.2 <X<322.2)`

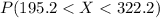
Using the z score we have:

`z = (322.2 -258.7)/(63.5)= 1`

`z = (195.2 -258.7)/(63.5)= -1`

And within one deviation from the mean we have 68% of the values