Question

Dwie proste przecinają się, tworząc kąty ostre i rozwarte. Miara kąta ostrego jest dwukrotnie mniejsza od miary kąta rozwartego. Oblicz miarę kąta rozwartego daje naj

Answer 1

The obtuse angle is 120°.

The acute angle is 60°.

Explanation:

This problem is about two crossing line, when that happens, we have 4 angles, two acute and two obtuse, where adjacent angles are supplementary and vertical angles are equal.

We can form the expression

`A = (O)/(2)`

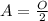
Where
`A` is an acute angle and
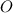`O` is an obtuse angle.}

Using all the given information, we have

`O + (O)/(2)=180\°`

Solving for
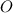`O`, we have

`(3O)/(2)=180\\ O=120\°`

Therefore, the obtuse angle is 120°, which means the acute angle is 60°, because they are supplementary angles, as we said befor.