Question

average of a data set was 40, and that standard deviation was 10, what else could you derive from that information.

Answer 1

`\bar x = 40, s =10`

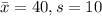
And from these values we can estimate the sample variance like this:

`s^2 = 10^2 =100`

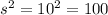
And we can also estimate the coeffcient of variation given by:

`\hat{CV} =(s)/(\bar x)`

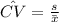
And replacing we got:

`\hat{CV} = (10)/(40)= 0.25`

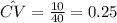
And this coefficient is useful in order to see the variability in terms of the mean for this case since is lower than 1 we can conclude that this variation around the mean is low.

Explanation:

For this case we have the following info given:

`\bar x = 40, s =10`

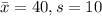
And from these values we can estimate the sample variance like this:

`s^2 = 10^2 =100`

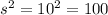
And we can also estimate the coeffcient of variation given by:

`\hat{CV} =(s)/(\bar x)`

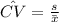
And replacing we got:

`\hat{CV} = (10)/(40)= 0.25`

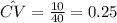
And this coefficient is useful in order to see the variability in terms of the mean for this case since is lower than 1 we can conclude that this variation around the mean is low.