Question

A particle oscillates between the points x=40 mm and x=160 mm with

an acceleration a =
k(100 - x), where a and x are expressed in mm/s2 and
respectively, and k is a constant. The velocity of the particle is 18 mm/s when x = 100 mm
and is zero at both x = 40 mm and x = 160 mm. Determine (a) the value of k,
(b) the velocity when x = 120 mm.​

Answer 1

(a) k = 0.09 s⁻¹

(b) The velocity= ± 16.97 mm/s

Step-by-step explanation:

(a) Given that the acceleration = a = k(100 - x)

Therefore;

`a = (dv)/(dt) = (dv)/(dx) * (dx)/(dt) = (dv)/(dx) * v = k(100 - x)`

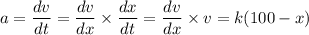
When x = 40 mm, v = 0 mm/s hence;

`\int\limits^v_0 {v } \, dv = \int\limits^x_(40) {k(100 - x)} \, dx`

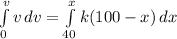
`(1)/(2) v^2 = k \cdot \left [100\cdot x-(1)/(2)\cdot x^(2) \right ]_(x)^(40)`

`(1)/(2) v^2 = -( k\cdot \left (x^(2)-200\cdot x+6400 \right ) )/(2)`

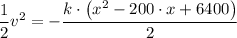
At x = 100 mm, v = 18 mm/s hence we have;

`(1)/(2) 18^2 = -( k\cdot \left (100^(2)-200* 100+6400 \right ) )/(2) = 1800\cdot k`

`(1)/(2) 18^2 =162 = 1800\cdot k`

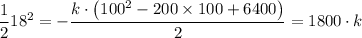
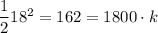
k = 162/1800 = 9/100 = 0.09 s⁻¹

(b) When x = 120 mm, we have

`(1)/(2) v^2 = -( 0.09* \left (120^(2)-200* 120+6400 \right ) )/(2) = 144`

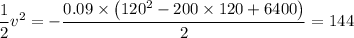
Therefore;

v² = 2 × 144 = 288

The velocity, v = √288 = ±12·√2 = ± 16.97 mm/s.