Question

A baker is folding up open-topped boxes to package up her baked goods. She has

flat, rectangular pieces of cardboard that are 10 inches by 6 inches. She wants to

maximize the volume of the box. What size squares should she cut from the corners

of the cardboard?

Answer 1

She should cut 1.21 inches (or a square of area 1.46 inch²) from 4 corners to get the maximum volume

Explanation:

Length = L = 10 inches

Width = W = 6 inches

Suppose x is cut from the 4 corners to make a box.

Dimensions of the Box:

L= 10 - 2x

W = 6 - 2x

H = x

Volume of the Box:

V = (L)(W)(H)

V = (10-2x)(6-2x)(x)

V = 4x³ - 32x² + 60x

For Maximum value:

`(dV)/(dx)=0`

`(dV)/(dx)=(d)/(dx)(4x^3-32x+60x)\\(dV)/(dx)=12x^2-64x+60\\12x^2-64x+60 = 0`

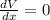
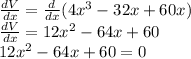
The values of x found are:

x= 4.12 , x = 1.21

If we put x= 4.12 in W= 6-2x , the value of width becomes negative, so that is not possible.

We discard 4.12. Now x=1.21

So,

If 1.21 inches are cut from 4 corners, or a square of 1.21*1.21 = 1.46 inch² is cut from 4 corners, we get the maximum value of V