Answer:
The half-life of the material is 2 years
Step-by-step explanation:
Given;
initial count rate = 2000 decays/minute
final count rate = 500 counts/min
decay time = Four hours
To determine the half life of the material; we create a simple decay table that matches the decay time and count rates.
time (years) count rate
0 2000 decays/minute
2 1000 decays/minute
4 500 decays/minute
Half life is the time intervals = 2 years
Also using a formula;
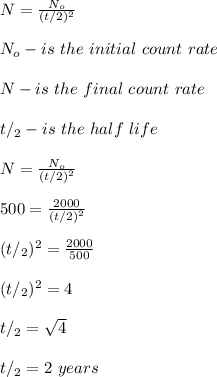
Therefore, the half-life of the material is 2 years