Question

A credit card had an APR of 15.98% all of last year, and compounded interest daily. What was the credit card's effective interest rate last year?

A.

17.32%


B.

17.20%


C.

16.96%


D.

16.62%

Answer 1

17.32%

Explanation:

Answer 2

Option(B) is the correct answer to the given question.

Step by Step Explanation

We know that

`A\ =\ P \ *(\ 1+\ (r)/(n) \ ) ^(nt)`

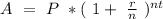
Here A=amount

r=15.98%=0.1598

n=365

t=1

Putting these values into the equation

`A\ =\ P \ *(\ 1+\ (0.1598)/(365) \ ) ^(365)`

`A\ =\ P \ *(\ 1+\ 0.000437) ^\ { 365}`

`A\ =\ P \ *(\ 1.000437 ) ^(365)`

`A\ =1.17288 P`

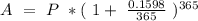
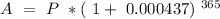
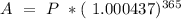
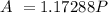
Now we find the interest

I=
`1.17288P\ -P\\=\ 0.17288P\\\ ~ 0.1720P`

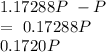
Therefore effective interest rate of the last year can be determined by

`(0.1720P)/(P)`

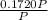
=0.1720 *100

=17.20%