Question

A supermarket is redesigning it’s checkout lanes. Design A has a sample size of 50, sample mean of 4.1 minutes, and sample standard deviation of 2.2 minutes. Design B has a sample size of 50, sample mean of 3.5 minutes, and sample standard deviation of 1.5 minutes. At the 0.05 level of significance, determine if their is evidence that the checkout times of the two systems differ.

Answer 1

The calculated value t = 1.57736 < 1.9845 at 5 % level of significance

Null hypothesis is accepted at 5 % level of significance

There is no significance difference between Design A and Design B

Explanation:

Given sample size of design A

n₁ = 50

sample mean of design A x⁻₁ = 4.1 minutes

Sample standard deviation S₁ = 2.2 minutes

Given sample size of design B

n₂ = 50

sample mean of design A x⁻₂ = 3.5 minutes

Sample standard deviation S₂ = 1.5 minutes

Null Hypothesis : H₀ : There is no significance difference between Design A and Design B

Alternative Hypothesis : H₁:There is significance difference between Design A and Design B

Level of significance ∝ = 0.05

Test statistic

`t = \frac{x^(-) _(1)- x^(-) _(2) }{\sqrt{S^(2) ((1)/(n_(1) )+(1)/(n_(2) )) } }`

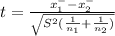
where

`S^(2) = (n_(1) S_(1) ^(2) +n_(2) S^2_(2) )/(n_(1) +n_(2) -2)`

`S^(2) = (50 (2.2)^(2) +50(1.5)^2)/(50+50-2)`

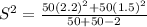
On calculation , we get

S² = 3.6173

Test statistic

`t = \frac{4.1-3.5}{\sqrt{3.617((1)/(50) +(1)/(50) }) }`

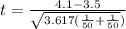
On calculation , we get

t = 1.57736

Degrees of freedom

ν = n₁ + n₂ -2 = 50 +50 -2 =98

t₀.₀₂₅ ,₉₈ = 1.9845

The calculated value t = 1.57736 < 1.9845 at 5 % level of significance

null hypothesis is accepted