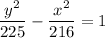Answer:
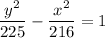
Explanation:
For a hyperbolic mirror the two foci are 42 cm apart.
The distance between the foci = 2c.
Therefore:
The distance of the vertex from one focus = 6 cm
The distance of the vertex from the other focus = 36 cm
2a=36-6=30
Now:
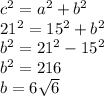
If the transverse axis lies on the y-axis, and the hyperbola is centered at the origin. Then the hyperbola has an equation of the form:

Therefore, the equation of the hyperbola is: