Question

A man pushes a 25kg box up an incline 2.0m by applying a steady force of 95N parallel to the incline. The box moves up the incline at a steady speed. The incline makes an angle 15 degrees to the horizontal

a) What is the force of friction between the incline and the box

b)If the box is released at the top of the incline, what will its speed be at the bottom

Answer 1

a) Ff = 19.29 N

b) v = 3.00 m/s

Step-by-step explanation:

a) To calculate the friction force you use the second Newton Law in the incline plane, with an acceleration equal to zero, because the motion of the box has a constant velocity:

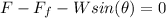`F-F_f-Wsin(\theta)=0\\\\` (1)

F: force applied by the man = 95N

Ff: friction force

W: weight of the box = Mg = (25kg)(9.8m/s^2) = 245N

θ: degree of the inclined plane = 15°

You solve the equation (1) for Ff and you replace the values of all variables in the equation (1):

`F_f=-Wsin(\theta)+F\\\\F_f=-(245N)sin18\°+95N=19.29N`

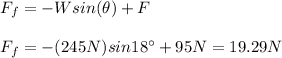
b) To fins the velocity of the box at the bottom you use the following formula:

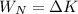`W_N=\Delta K` (2)

That is, the net work over the box is equal to the change in the kinetic energy of the box.

The net work is:

`W_N=Mgsin(18\°)d-Ffd`

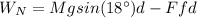
d: distance traveled by the box = 2.0m

`W_N=245sin18\°(2.0m)N-19.29(2.0m)N=112.83J`

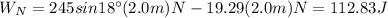
You use this value of the net work to find the final velocity of the box, by using the equation (2):

`112.8J=(1)/(2)m[v^2-v_o^2]\\\\v_o=0m/s\\\\v=\sqrt{(2(112.8J))/(m)}=\sqrt{(225.67J)/(25kg)}=3.00(m)/(s)`

The speed of the box, at the bottom of the incline plane is 3.00 m/s