Answer:
a) Ff = 19.29 N
b) v = 3.00 m/s
Step-by-step explanation:
a) To calculate the friction force you use the second Newton Law in the incline plane, with an acceleration equal to zero, because the motion of the box has a constant velocity:
 (1)
(1)
F: force applied by the man = 95N
Ff: friction force
W: weight of the box = Mg = (25kg)(9.8m/s^2) = 245N
θ: degree of the inclined plane = 15°
You solve the equation (1) for Ff and you replace the values of all variables in the equation (1):
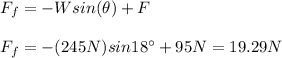
b) To fins the velocity of the box at the bottom you use the following formula:
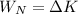 (2)
(2)
That is, the net work over the box is equal to the change in the kinetic energy of the box.
The net work is:
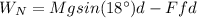
d: distance traveled by the box = 2.0m

You use this value of the net work to find the final velocity of the box, by using the equation (2):
![112.8J=(1)/(2)m[v^2-v_o^2]\\\\v_o=0m/s\\\\v=\sqrt{(2(112.8J))/(m)}=\sqrt{(225.67J)/(25kg)}=3.00(m)/(s)](https://img.qammunity.org/2021/formulas/physics/college/p0kp3bkldw3feplbwf3bgd1mnjxpgibj7b.png)
The speed of the box, at the bottom of the incline plane is 3.00 m/s