Question

Problem 10: A tank initially contains a solution of 10 pounds of salt in 60 gallons of water. Water with 1/2 pound of salt per gallon is added to the tank at 6 gal/min, and the resulting solution leaves at the same rate. Find the quantity Q(t) of salt in the tank at time t > 0.

Answer 1

The quantity of salt at time t is
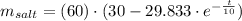`m_(salt) = (60)\cdot (30 - 29.833\cdot e^{-(t)/(10) })`, where t is measured in minutes.

Explanation:

The law of mass conservation for control volume indicates that:

`\dot m_(in) - \dot m_(out) = \left((dm)/(dt) \right)_(CV)`

Where mass flow is the product of salt concentration and water volume flow.

The model of the tank according to the statement is:

`(0.5\,(pd)/(gal) )\cdot \left(6\,(gal)/(min) \right) - c\cdot \left(6\,(gal)/(min) \right) = V\cdot (dc)/(dt)`

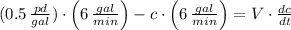
Where:

`c` - The salt concentration in the tank, as well at the exit of the tank, measured in
`(pd)/(gal)`.

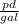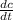`(dc)/(dt)` - Concentration rate of change in the tank, measured in
`(pd)/(min)`.

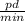`V` - Volume of the tank, measured in gallons.

The following first-order linear non-homogeneous differential equation is found:

`V \cdot (dc)/(dt) + 6\cdot c = 3`

`60\cdot (dc)/(dt) + 6\cdot c = 3`

`(dc)/(dt) + (1)/(10)\cdot c = 3`

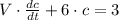
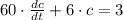
This equation is solved as follows:

`e^{(t)/(10) }\cdot \left((dc)/(dt) +(1)/(10) \cdot c \right) = 3 \cdot e^{(t)/(10) }`

`(d)/(dt)\left(e^{(t)/(10)}\cdot c\right) = 3\cdot e^{(t)/(10) }`

`e^{(t)/(10) }\cdot c = 3 \cdot \int {e^{(t)/(10) }} \, dt`

`e^{(t)/(10) }\cdot c = 30\cdot e^{(t)/(10) } + C`

`c = 30 + C\cdot e^{-(t)/(10) }`

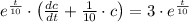
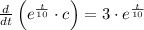
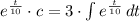
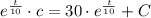
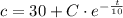
The initial concentration in the tank is:

`c_(o) = (10\,pd)/(60\,gal)`

`c_(o) = 0.167\,(pd)/(gal)`

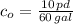
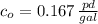
Now, the integration constant is:

`0.167 = 30 + C`

`C = -29.833`

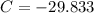
The solution of the differential equation is:

`c(t) = 30 - 29.833\cdot e^{-(t)/(10) }`

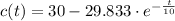
Now, the quantity of salt at time t is:

`m_(salt) = V_(tank)\cdot c(t)`

`m_(salt) = (60)\cdot (30 - 29.833\cdot e^{-(t)/(10) })`

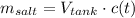
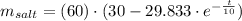
Where t is measured in minutes.