Question

A travel agent wants to determine how much the average client is willing to pay for a weekend at an all-expense paid resort. The agent surveys 30 clients and finds that the average willingness to pay is $2,500 with a standard deviation of $840. However, the travel agent is not satisfied and wants to be 95% confident that the sample mean falls within $150 of the true average. What is the minimum number of clients the travel agent should survey

Answer 1

`n=((1.960(840))/(150))^2 =120.47 \approx 121`

So the answer for this case would be n=12 rounded up to the next integer

Step-by-step explanation:

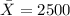`\bar X=2500` represent the sample mean

`\mu` population mean (variable of interest)

s=840 represent the sample standard deviation

n represent the sample size

The margin of error is given by this formula:

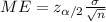`ME=z_(\alpha/2)(\sigma)/(√(n))` (a)

And on this case we have that ME =150 and we are interested in order to find the value of n, if we solve n from equation (a) we got:

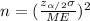`n=((z_(\alpha/2) \sigma)/(ME))^2` (b)

The critical value for 95% of confidence interval, the significance level if 5% and the critical value would be
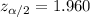`z_(\alpha/2)=1.960`, replacing into formula (b) we got:

`n=((1.960(840))/(150))^2 =120.47 \approx 121`

So the answer for this case would be n=12 rounded up to the next integer