Answer:
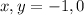
Explanation:
System of Linear Equations entered :
[1] 3x + 4y = -3
[2] x + 2y = -1
Solve by Substitution :
// Solve equation [2] for the variable x
[2] x = -2y - 1
// Plug this in for variable x in equation [1]
[1] 3•(-2y-1) + 4y = -3
[1] - 2y = 0
// Solve equation [1] for the variable y
[1] 2y = 0
[1] y = 0
// By now we know this much :
x = -2y-1
y = 0
// Use the y value to solve for x
x = -2(0/32765)-1 = -1
Solution :
{x,y} = {-1,0/32765}