Question

A 4.0 kg block is initially at rest on a frictionless, horizontal surface. The block is moved 8.0 m by the application of a constant 10.0 N horizontal force. If the block slides into a fixed horizontal spring and comes to rest when the spring is compressed a distance of x=0.25m. Determine the spring constant of the fixed horizontal spring. Show all formula with substitutions and units.

Answer 1

k = 2560 N/m

Step-by-step explanation:

To find the spring constant, you take into account that all the kinetic energy of the block becomes elastic potential energy in the spring, when the block compressed totally the spring:

`K=U\\\\(1)/(2)mv^2=(1)/(2)kx^2`

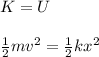
m: mass of the block = 4.0kg

v: velocity of the block just before it hits the spring

x: compression of the spring = 0.25m

k: spring constant = ?

You solve the previous equation for k:

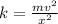`k=(mv^2)/(x^2)` (1)

Then, you have to calculate the velocity v of the block. First, you calculate the acceleration of the block by using the second Newton law:

`F=ma`

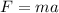
F: force over the block = 10.0N

a: acceleration

`a=(F)/(m)=(10.0N)/(4.0kg)=2.5(m)/(s^2)`

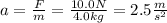
With this value of a you can calculate the final velocity after teh block has traveled a distance of 8.0m:

`v^2=v_o^2+2ad`

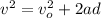
vo: initial velocity = 0m/s

d: distance = 8.0m

`v=√(2ad)=√(2(2.5m/s^2)(8.0m))=6.32(m)/(s)`

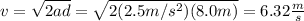
Now, you can calculate the spring constant by using the equation (1):

`k=(mv^2)/(x^2)=((4.0kg)(6.32m/s)^2)/((0.25m)^2)=2560(N)/(m)`

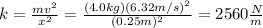
hence, the spring constant is 2560 N/m