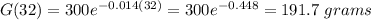Question

At the beginning of an experiment, a scientist has 300 grams of radioactive goo. After 150 minutes, her sample has decayed to 37.5 grams.

What is the half-life of the goo in minutes?


________



Find a formula for


G(t),


the amount of goo remaining at time T.


G= _________



How many grams of goo will remain after 32 minutes?

Answer 1

Half-life of the goo is 49.5 minutes

`G(t)= 300e^(-0.014t)`

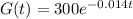
191.7 grams of goo will remain after 32 minutes

Explanation:

Let
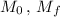`M_0\,,\,M_f` denotes initial and final mass.

`M_0=300\,\,grams\,,\,M_f=37.5\,\,grams`

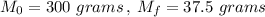
According to exponential decay,

`\ln \left ( (M_f)/(M_0) \right )=-kt`

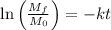
Here, t denotes time and k denotes decay constant.

`\ln \left ( (M_f)/(M_0) \right )=-kt\\\ln \left ( (37.5)/(300) \right )=-k(150)\\-2.079=-k(150)\\k=(2.079)/(150)=0.014`

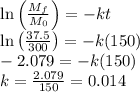
So, half-life of the goo in minutes is calculated as follows:

`\ln \left ( (50)/(100) \right )=-kt\\\ln \left ( (50)/(100) \right )=-(0.014)t\\t=(-0.693)/(-0.014)=49.5\,\,minutes`

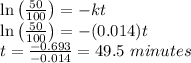
Half-life of the goo is 49.5 minutes

`\ln \left ( (M_f)/(M_0) \right )=-kt\Rightarrow M_f=M_0e^(-kt)`

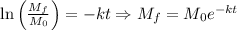
So,

`G(t)= M_f=M_0e^(-kt)`

Put
`M_0=300\,\,grams\,,\,k=0.014`

`G(t)= 300e^(-0.014t)`

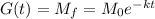
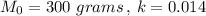
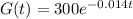
Put t = 32 minutes

`G(32)= 300e^(-0.014(32))=300e^(-0.448)=191.7\,\,grams`