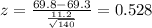Answer:
Part a
Null hypothesis:
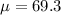
Alternative hypothesis:
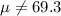
Part b
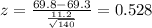
Explanation:
For this case we have the following info given :
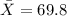 the sample mean
the sample mean
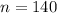 represent the sample size
represent the sample size
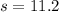 represent the standard deviation
represent the standard deviation
Part a
And we want to test if the true mean is equal to 69.3 so then the system of hypothesis:
Null hypothesis:
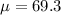
Alternative hypothesis:
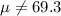
Part b: Find the statistic
The statistic is given by:
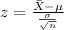
And replacing the info we got: