The coordinate of point
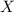 inside segment
inside segment
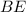 that is
that is
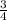 the distance from
the distance from
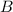 to
to
 is at
is at
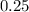 on the number line.
on the number line.
To find the coordinate of point X inside segment BE that is \( \frac{3}{4} \) the distance from B to E:
1. Determine the coordinates of points B and E on the number line.
2. Calculate the total distance between B and E.
3. Multiply the total distance by
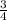 to find
to find
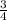 of the distance from B.
of the distance from B.
4. Add this distance to the coordinate of B to find the coordinate of X.
From the image, it's difficult to read the exact coordinates of B and E, but it appears that B is at -5 and E is at 2. Let's calculate it:
- Total distance between B and E:
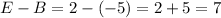
-
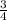 of the distance:
of the distance:
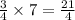
- Coordinate of X:
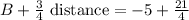
Let's calculate the exact coordinate of X.
The coordinate of point
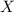 inside segment
inside segment
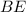 that is
that is
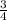 the distance from
the distance from
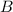 to
to
 is at
is at
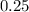 on the number line.
on the number line.