Question

The temperature of a flowing gas is to be measured with a thermocouple junction and wire stretched between two legs of a sting, a wind tunnel test fixture. The junction is formed by butt-welding two wires of different material. For wires of diameter D = 125 m and a convection coefficient of h = 700 W/m^2 K, determine the minimum separation distance between the two legs of the sting, L=L1+L2, to ensure that the sting temperature does not influence the junction temperature and, in turn, invalidate the gas temperature measurement. Consider two different types of thermocouple junctions consisting of (i) copper and constantan wires and (ii) chromel and aluminel wires. Evaluate the thermal conductivity of copper and constantan at T300 K. Use kCh =19 W/mK and kA = l29 W/mK for the thermal conductivities of the chromel and alumel wires, respectively.

Answer 1

• minimum separation distance between the two legs of the sting L = L 1 + L 2 therefore L = 9.48 + 4.68 = 14.16 m

• L = 1.14 m

Step-by-step explanation:

D ( diameter ) = 125 m

convection coefficient of h = 700 W/m^2

Calculate THE CROSS SECTIONAL AREA

Ac =
`(\pi )/(4) * D^2` =
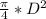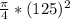`(\pi )/(4) * ( 125 )^2` = 0.79 * 15625 = 12343.75 m^2

perimeter

p =
`\pi * D` = 3.14 * 125 = 392.5 m

at 300k temperature the thermal conductivity of copper and constantan from the thermodynamic property table are :

Kcu = 401 w/m.k

Kconstantan = 23 W/m.k

To calculate the length of copper wire of the thermocouple junction

L 1 = 4.6 (
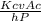`(Kcv Ac)/(h P)`) ^ 1/2 = 4.6
`((401 *12343.75 )/(700 *392.5))^(1)/(2)`

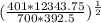
L 1 = 4.6 ( 4949843.75 / 274750 )^1/2

L 1 = 9.48 m

calculate length of constantan wire

L 2 = 4.6
`((kcons*Ac)/(hp) )^(1)/(2)`

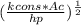
= 4.6 ( (23 * 12343.75) / ( 700 * 392.5) ) ^1/2

L 2 = 4.6 ( 283906.25 / 274750 ) ^ 1/2

L 2 = 4.68 m

I) therefore the minimum separation distance between the two legs of the sting L = L 1 + L 2

L = 9.48 + 4.68 = 14.16 m

ii) Evaluating the thermal conductivity of copper and constantan

Kc ( thermal conductivity of chromel) = 19 w/m.k

Ka ( thermal conductivity of alumel ) = 29 W/m.k

distance between the legs L = L 1 + L 2

THEREFORE

L = 4.6 ( (Kcn * Ac ) / ( hp ) )^1/2 + 4.6 ( (Kac * Ac)/(hp) )^1/2

L = 4.6
`((Ac)/(hp) )^(1)/(2) [ (Kcn)^(1)/(2) + (Kal)^(1)/(2) ]`

L = 4.6 ( 12343.75 /( 700 * 392.5) )^1/2 * [ 19^1/2 + 29^1/2 ]

L = 4.6 ( 12343.75 / 274750 ) ^1/2 * 5.39

L = 1.14 m