Answer:
Explanation:
Given that:
68.87, 78.25, 70.44, 84.67, 79.79, 86.33, 100.24, 98.26
we calculate sample mean and standard deviation from given data
Sample Mean
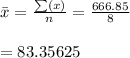
Sample Variance

sample standard deviation
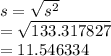
95% CI for
 using t - dist
using t - dist
Sample mean = 83.35625
Sample standard deviation = 11.546334
Sample size = n = 8
Significance level = α = 1 - 0.95 = 0.05
Degrees of freedom for t - distribution
d-f = n - 1 = 7
Critical value
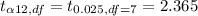 ( from t - table , two tails, d.f =7)
( from t - table , two tails, d.f =7)
Margin of Error
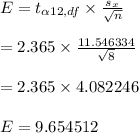
Limits of 95% Confidence Interval are given by:
Lower limit
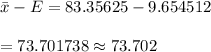
Upper Limit
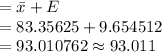
95% Confidence interval is
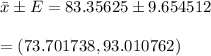
95% CI using t - dist (73.70 < μ < 93.01)
D. The lower bound is $ and the upper bound is One can be [95]% confident that the mean travel tax for all cities is between these values.
c.What would you recommend to a researcher who wants to increase the precision of the interval, but does not have access to additional data?
A. The researcher could decrease the level of confidence.