Question

Find the length of both of the unknown sides in the triangle shown here.

Give your answer correct to the nearest metre. [5 marks]

Answer 1

`(x+11)^2 = (x+3)^2 +16^2`

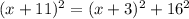
And if we solve this equation for x we got:

`x^2 +22x +121 = x^2 +6x +9 +256`

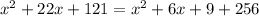
We can cancel
`x^2` in both sides and we have this:

`22x -6x= 256+9-121 =144`

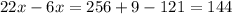
And then we got:

`16 x= 144`

`x =(144)/(16)= 9`

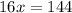
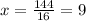
And then the length of the sides are 9+11= 20 m for the hypothenuse, 16 for the adjacent side and 9+3 = 12m for the last side.

Lenght of the smaller unknown side: 12m

Lenght of the larger unknown side: 20m

Explanation:

For this case we have a right triangle and we can use the Pythagoras Theorem and using the info given by the triangle we can set up the following equation:

`(x+11)^2 = (x+3)^2 +16^2`

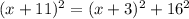
And if we solve this equation for x we got:

`x^2 +22x +121 = x^2 +6x +9 +256`

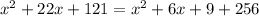
We can cancel
`x^2` in both sides and we have this:

`22x -6x= 256+9-121 =144`

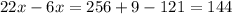
And then we got:

`16 x= 144`

`x =(144)/(16)= 9`

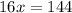
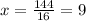
And then the length of the sides are 9+11= 20 m for the hypothenuse, 16 for the adjacent side and 9+3 = 12m for the last side side.

Lenght of the smaller unknown side: 12m

Lenght of the larger unknown side: 20m