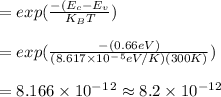Question

Crystalline germanium (Z=32, rho=5.323 g/cm3) has a band gap of 0.66 eV. Assume the Fermi energy is half way between the valence and conduction bands. Estimate the ratio of electrons in the conduction band to those in the valence band at T = 300 K. (See eq. 10-11) Assume the width of the valence band is ΔΕV ~ 10 eV.

Answer 1

= 8.2*10⁻¹²

Step-by-step explanation:

Probability of finding an electron to occupy a state of energy, can be expressed by using Boltzmann distribution function

`f(E) = exp(-(E-E_f)/(K_BT) )`

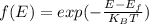
From the given data, fermi energy lies half way between valence and conduction bands, that is half of band gap energy

`E_f = (E_g)/(2)`

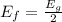
Therefore,

`f(E) = exp(-(E-(E_g)/(2) )/(K_BT) )`

Using boltzman distribution function to calculate the ratio of number of electrons in the conduction bands of those electrons in the valence bond is

`(n_(con))/(n_(val)) =(exp(-([E_c-E_g/2])/(K_BT) ))/(exp(-([E_v-E_fg/2)/(K_BT) ))`

`= exp((-(E_c-E_v)/(K_BT) )\\\\=exp((-(0.66eV))/((8.617*10^-^5eV/K)(300K)) )\\\\=8.166*10^-^1^2\approx8.2*10^(-12)`