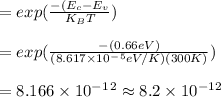Answer:
= 8.2*10⁻¹²
Step-by-step explanation:
Probability of finding an electron to occupy a state of energy, can be expressed by using Boltzmann distribution function
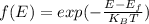
From the given data, fermi energy lies half way between valence and conduction bands, that is half of band gap energy
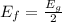
Therefore,
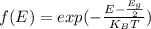
Using boltzman distribution function to calculate the ratio of number of electrons in the conduction bands of those electrons in the valence bond is
![(n_(con))/(n_(val)) =(exp(-([E_c-E_g/2])/(K_BT) ))/(exp(-([E_v-E_fg/2)/(K_BT) ))](https://img.qammunity.org/2021/formulas/physics/college/u5kvmlnkwaqtei9rohi5ansr57nzt0wgss.png)