Answer:
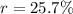 will ensure that accumulated amount at the end of one year is 1.5 times more than amount invested
will ensure that accumulated amount at the end of one year is 1.5 times more than amount invested
Explanation:
Given: An amount was invested at r% per quarter.
To find: value of r such that accumulated amount at the end of one year is 1.5 times more than amount invested
Solution:
Let P denotes amount invested and n denotes time
As an amount (A) was invested at r% per quarter,
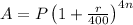
According to question, accumulated amount at the end of one year is 1.5 times more than amount invested.
So,
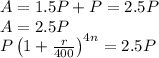
Put n = 1
![P\left ( 1+(r)/(400) \right )^(4)=2.5P\\\left ( 1+(r)/(400) \right )^(4)=2.5\\1+(r)/(400) =(2.5)^{(1)/(4)}\\(r)/(100)=(2.5)^{(1)/(4)}-1\\r=100\left [ (2.5)^{(1)/(4)}-1 \right ]\\=25.7\%](https://img.qammunity.org/2021/formulas/mathematics/college/k2i4bd4u3dk7hx6q6vr9ibgocpg96nyvcw.png)