Question

The point-slope form of the equation of the line that passes through (-9, -2) and (1, 3) is y– 3 = {(x - 1). What is the

slope-intercept form of the equation for this line?

Answer 1

The Answer is C

Explanation:

i think This is correct

Answer 2

`y=(1)/(2)x+(5)/(2)`.

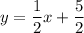Explanation:

If a line passing through two points, then the equation of line is

`(y-y_1)=(y_2-y_1)/(x_2-x_1)(x-x_1)`

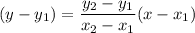
It is given that the passing through (1,3) and (-9,-2). So, equation of line in point slope form is

`\Rightarrow (y-3)=(-2-3)/(-9-1)(x-1)`

`\Rightarrow (y-3)=(1)/(2)(x-1)`

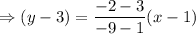
Slope intercept form of a line is

`y=mx+b`

where, m is slope and b is y-intercept.

Now,

`(y-3)=(1)/(2)(x-1)`

`\Rightarrow (y-3)=(1)/(2)(x}-(1)/(2)(1)`

`\Rightarrow y=(1)/(2)(x}-(1)/(2)+3`

`\Rightarrow y=(1)/(2)x+(5)/(2)`

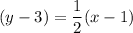
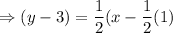
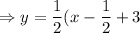
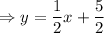
Therefore, the required equation is
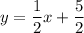`y=(1)/(2)x+(5)/(2)`.