Question

A string is stretched between fixed supports separated by 72.0 cm. It is observed to have resonant frequencies of 370 and 555 Hz, and no other resonant frequencies between these two.(a) What is the lowest resonant frequency for this string?(b) What is the wave speed for this string?

Answer 1

(a) f = 185 Hz

(b) v = 266.4 m/s

Step-by-step explanation:

(a) The lowest frequency can be calculated by using the following formula for the calculation of the modes (resonant frequencies) in a string:

`f_n=(nv)/(2L)`

`f_n=nf`

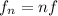
n: order of the mode

v: velocity of the waves in the string

L: length of the string = 72.0cm = 0.72m

fn: frequency of the n-th mode

With the information about two consecutive modes you can find the lowest resonant frequency. First you find the resonant mode n:

`f_n=nf\\\\f_(n-1)=(n-1)f\\\\(f_n)/(f_(n-1))=(n)/(n-1)`

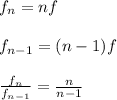
you solve the previous equation for n:

`(n-1)f_n=nf_(n-1)\\\\555n-555=370n\\\\n=3`

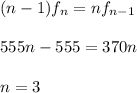
With this information you can calculate the lowest resonant frequency:

`f_n=nf\\\\f=(f_n)/(n)=(555)/(3)=185Hz`

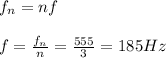
b) You have information about two consecutive modes fn, fn-1. Then, you can calculate the velocity of the waves:

`f_(n)-f_(n-1)=n(v)/(2L)-(n-1)(v)/(2L)\\\\f_n-f_(n-1)=(v)/(2L)\\\\v=2L(f_n-f_(n-1))`

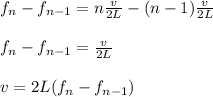
fn = 555 Hz

fn-1: 370 Hz

`v=2(0.72m)(555-370)Hz=266.4(m)/(s)`´

hence, the velocityof the waves in the string is 266.4 m/s