Answer:
Explanation:
From the question; we are given the following inclusive frequency distribution information
Class Frequency f
1.1-1.5 18
1.6-2.0 27
2.1-2.5 31
2.6-3.0 40
3.1-3.5 56
3.6-4.0 55
4.1-4.5 23
Convert the above inclusive frequency distribution to exclusive frequency distribution with respect of the upper and lower class limit ; we have:
Class Frequency f
1.05 - 1.55 18
1.55 - 2.05 27
2.05 - 2.55 31
2.55 - 3.05 40
3.05 - 3.55 56
3.55 - 4.05 55
4.05 - 4.55 23
Class Frequency f cf
1.05 - 1.55 18 18
1.55 - 2.05 27 45
2.05 - 2.55 31 76
2.55 - 3.05 40 116
3.05 - 3.55 56 172
3.55 - 4.05 55 227
4.05 - 4.55 23 250
n = 250
To determine the daily sales; we can derive that from estimated Mode by using the relation :
Estimated Mode = L + fm − fm-1(fm − fm-1) + (fm − fm+1) × w
here:
L = the lower class boundary of the modal group
fm-1 = the frequency of the group before the modal group
fm = the frequency of the modal group
fm+1 = the frequency of the group after the modal group
w = the group width
However;
It is easier now to determine the modal group (i.e the group with the highest frequency), which is 3.05 -3.55
L = 3.05
fm-1 =40
fm =56
fm+1 = 55
w = 0.5
∴

To find Median Class ; we use the formula;
Median Class = value of (n / 2)th observation
Median Class = value of (250 / 2)th observation
Median Class = value of 125th observation
From the column of cumulative frequency cf,
we will see that the 125th observation lies in the class 3.05-3.55.
∴ The median class is 3.05-3.55.
Thus;,
L=lower boundary point of median class =3.05
n=Total frequency =250
cf=Cumulative frequency of the class preceding the median class =116
f=Frequency of the median class =56
c=class length of median class =0.5
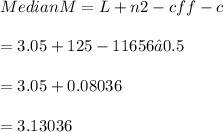
hence median sales = $3130.36