Answer:
x2−10 because the area expression can be rewritten as (x2−10)(x2+10) which equals (x2−10)((x2−10)+20).
Explanation:
The area of the rectangle is
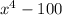 , which can be factored as
, which can be factored as
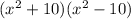 , because it's the difference of two perfect squares.
, because it's the difference of two perfect squares.
But, we know that
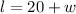 , where
, where
 is the length and
is the length and
 is the width.
is the width.
Additionally,
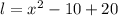 and
and
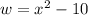 , which means
, which means
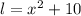 .
.
Therefore, the right answer is A.