Question

For the given set, first calculate the number of subsets for the set, then calculate the

{5, 13, 17, 20}
The number of subsets is ]
The number of proper subsets is .

Answer 1

`\fbox{\begin{minipage}{14em}Number of subsets: 16\\Number of proper subsets: 15\end{minipage}}`

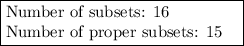
Explanation:

Given:

The set A = {5, 13, 17, 20}

Question:

Find the number of subsets of A

Find the number of proper subsets of A

Simple solution by counting:

Subset of A that has 0 element:

{∅} - 1 set

Subset of A that has 1 element:

{5}, {13}, {17}, {20} - 4 sets

Subset of A that has 2 elements:

{5, 13}, {5, 17}, {5, 20}, {13, 17}, {13, 20}, {17, 20} - 6 sets

Subset of A that has 3 elements:

{5, 13, 17}, {5, 13, 20}, {5, 17, 20}, {13, 17, 20} - 4 sets

Subset of A that has 4 elements:

{5, 13, 17, 20} - 1 set

In total, the number of subsets of A: N = 1 + 4 + 6 + 4 + 1 = 16

The number of proper subsets (all of subsets, except subset which is equal to original set A): N = 16 - 1 = 15

Key-point:

The counting method might be used for finding the number of subsets when the original set contains few elements.

The question is that, for a set that contains many elements, how to find out the number of subsets?

The answer is that: there is a fix formula to calculate the total number (
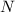`N`) of subsets of a set containing
`n` elements: N =
`2^(n)`

With original set A = {5, 13, 17, 20}, there are 4 elements belonged to A.

=> Number of subsets of A: N =
`2^(4) = 16`

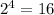
(same result as using counting method)

Brief proof of formula: N =
`2^(n)`

Each element of original set is considered in 2 status: existed or not.

If existed => fill that element in.

If not => leave empty.

For i.e.: empty subset means that all elements are selected as not existed, subset with 1 element means that all elements are selected as not existed, except 1 element, ... and so on.

=> From the point of view of a permutation problem, for each element in original set, there are 2 ways to select: existed or not. There are
`n` elements in total. => There are
`2^n}` ways to select, or in other words, there are
`2^(n)` subsets.

Hope this helps!

:)