Answer:
1) The normal reactions at the front wheel is 9909.375 N
The normal reactions at the rear wheel is 8090.625 N
2) The least coefficient of friction required between the tyres and the road is 0.625
Step-by-step explanation:
1) The parameters given are as follows;
Speed, u = 90 km/h = 25 m/s
Distance, s it takes to come to rest = 50 m
Mass, m = 1.8 tonnes = 1,800 kg
From the equation of motion, we have;
v² - u² = 2·a·s
Where:
v = Final velocity = 0 m/s
a = acceleration
∴ 0² - 25² = 2 × a × 50
a = -6.25 m/s²
Force, F = mass, m × a = 1,800 × (-6.25) = -11,250 N
The coefficient of friction, μ, is given as follows;
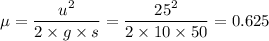
Weight transfer is given as follows;
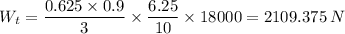
Therefore, we have for the car at rest;
Taking moment about the Center of Gravity CG;
 × 1.3 = 1.7 ×
× 1.3 = 1.7 ×
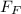
 +
+
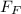 = 18000
= 18000
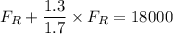
 = 18000*17/30 = 10200 N
= 18000*17/30 = 10200 N
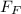 = 18000 N - 10200 N = 7800 N
= 18000 N - 10200 N = 7800 N
Hence with the weight transfer, we have;
The normal reactions at the rear wheel
 = 10200 N - 2109.375 N = 8090.625 N
= 10200 N - 2109.375 N = 8090.625 N
The normal reactions at the front wheel
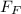 = 7800 N + 2109.375 N = 9909.375 N
= 7800 N + 2109.375 N = 9909.375 N
2) The least coefficient of friction, μ, is given as follows;
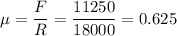
The least coefficient of friction, μ = 0.625.