Question

Solve the equation and show your work.

A . 17x + 12 = 54 - 4x

B . 5x - 10 + 2x = 6(x + 1) - x

Answer 1

Hey ! there

Answer:

• Value of x in equation A is 2 .

• Value of x in equation B is 8 .

Explanation:

In this question we are provided with two equations that are 17x + 12 = 54 - 4x and 5x - 10 + 2x = 6(x + 1) - x . And we are asked to solve the equation that means we have to find the value of x for both the equations .

Solution : -

A)

`\longmapsto \qquad \: 17x + 12 = 54 - 4x`

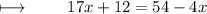
Step 1 : Subtracting 12 on both sides :

`\longmapsto \qquad \: 17x + \cancel{ 12} - \cancel{12} = \bold{54} - 4x - \bold{ 12}`

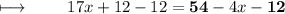
Simplifying it ,

`\longmapsto \qquad \: 17x = 42 - 4x`

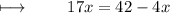
Step 2 : Adding 4x on both sides :

`\longmapsto \qquad \: 17x + 4x = 42 - \cancel{4x} + \cancel{4x}`

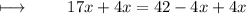
On further calculations, we get :

`\longmapsto \qquad \: 21x = 42`

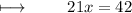
Step 3 : Dividing with 21 on both sides :

`\longmapsto \qquad \: \frac{ \cancel{21}x}{ \cancel{21} } = \cancel{ (42)/(21) }`

We get :

`\longmapsto \qquad \: \red{\underline{\boxed{ \frak{x = 2}}}} \quad \bigstar`

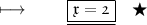
• Henceforth , value of x is 2 .

Verifying : -

Now , we are verifying our answer by substituting value of x as 2 in the given equation . So ,

• 17x + 12 = 54 - 4x

• 17 ( 2 ) + 12 = 54 - 4 ( 2 )

• 34 + 12 = 54 - 8

• 46 = 46

• L.H.S = R.HS

• Hence , Verified .

Therefore , our solution is correct .

▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬

B)

`\longmapsto \qquad \: 5x - 10 + 2x = 6(x + 1) - x`

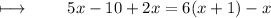
Step 1 : Adding like terms on left side :

`\longmapsto \qquad \: 7x - 10 = 6(x + 1) - x`

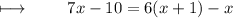
Step 2 : Solving parenthesis on right side by using distributive property . ( Multiplying 6 with x and 1 both ) :

`\longmapsto \qquad \: 7x - 10 = \bold{6x} + 6 - \bold{x}`

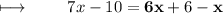
Step 3 : Solving like terms on right side :

`\longmapsto \qquad \: 7x - 10 = 5x + 6`

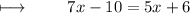
Step 4 : Adding 10 on both sides :

`\longmapsto \qquad \: 7x - \cancel{10} + \cancel{ 10} = 5x + 6 + 10`

Simplifying it ,

`\longmapsto \qquad \: 7x = 5x + 16`

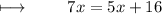
Step 5 : Subtracting 5x on both sides :

`\longmapsto \qquad \: 7x - 5x = \cancel{5x }+ 16 - \cancel{5x}`

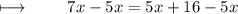
On further calculations , we get :

`\longmapsto \qquad \: 2x = 16`

Step 6 : Dividing with 2 on both sides :

`\longmapsto \qquad \: \frac{ \cancel{2}x}{ \cancel{2}} = \cancel{(16)/(2) }`

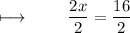
We get :

`\longmapsto \qquad \: \red{\underline{\boxed{ \frak{x = 8}}} } \quad \bigstar`

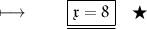
• Henceforth , value of x is 8 .

Verifying : -

Now , we are verifying our answer by substituting value of x as 8 in the given equation . So ,

• 5x - 10 + 2x = 6(x + 1) - x

• 5 ( 8 ) - 10 + 2( 8 ) = 6 ( 8 + 1 ) - 8

• 40 ( - 10 ) + 16 = 6 ( 9 ) - 8

• 56 - 10 = 54 - 8

• 46 = 46

• L.H.S = R.H.S

• Hence , Verified .

Therefore , our solution is correct.

#Keep Learning

Answer 2

A. x= 2

B. x= 8

Explanation:

Solving an equation refers to finding the value of the variable in the equation.

A. 17x +12= 54 -4x

Bring all x terms to one side, constant to the other:

17x +4x= 54 -12

21x= 42

x= 42 ÷21

x= 2

B. 5x -10 +2x= 6(x +1) -x

7x -10= 6x +6 -x

7x -10= 5x +6

Bring all x terms to one side, constant to the other:

7x -5x= 10 +6

2x= 16

Divide both sides by 2:

x= 16 ÷2

x= 8