Hey ! there
Answer:
- Value of x in equation A is 2 .
- Value of x in equation B is 8 .
Explanation:
In this question we are provided with two equations that are 17x + 12 = 54 - 4x and 5x - 10 + 2x = 6(x + 1) - x . And we are asked to solve the equation that means we have to find the value of x for both the equations .
Solution : -
A)
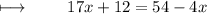
Step 1 : Subtracting 12 on both sides :
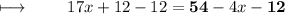
Simplifying it ,
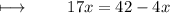
Step 2 : Adding 4x on both sides :
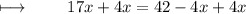
On further calculations, we get :
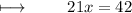
Step 3 : Dividing with 21 on both sides :
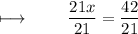
We get :
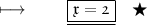
- Henceforth , value of x is 2 .
Verifying : -
Now , we are verifying our answer by substituting value of x as 2 in the given equation . So ,
- 17 ( 2 ) + 12 = 54 - 4 ( 2 )
Therefore , our solution is correct .
▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬▬
B)
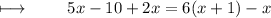
Step 1 : Adding like terms on left side :
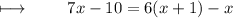
Step 2 : Solving parenthesis on right side by using distributive property . ( Multiplying 6 with x and 1 both ) :
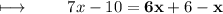
Step 3 : Solving like terms on right side :
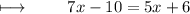
Step 4 : Adding 10 on both sides :
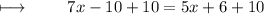
Simplifying it ,
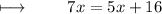
Step 5 : Subtracting 5x on both sides :
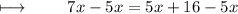
On further calculations , we get :
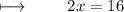
Step 6 : Dividing with 2 on both sides :
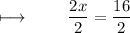
We get :
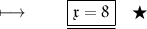
- Henceforth , value of x is 8 .
Verifying : -
Now , we are verifying our answer by substituting value of x as 8 in the given equation . So ,
- 5x - 10 + 2x = 6(x + 1) - x
- 5 ( 8 ) - 10 + 2( 8 ) = 6 ( 8 + 1 ) - 8
- 40 ( - 10 ) + 16 = 6 ( 9 ) - 8
Therefore , our solution is correct.
#Keep Learning