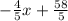Question

X^2+4x+y^2-10y+20=30 find the center of the circle by completing the square

Answer 1

a). Center of the circle = (-2, 5)

b). Equation of the line ⇒ y =
`-(4)/(5)x+(58)/(5)`

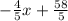
Explanation:

Equation of the circle is,

x² + 4x + y²- 10y + 20 = 30

a). [x² + 2(2)x + 4 - 4] + [y²- 2(5)y + 25] - 25 + 20 = 30

[x² + 2(2)x + 4] - 4 + [y² - 2(5)y + 25] - 25 + 20 = 30

(x + 2)² + (y - 5)²- 29 + 20 = 30

(x + 2)² + (y - 5)²- 9 = 30

(x + 2)² + (y - 5)² = 39

By comparing this equation with the standard equation of a circle,

Center of the circle is (-2, 5).

b). A point (2, 10) lies on this circle.

Slope of the line joining this point to the center (-2, 5),

`m_(1)=(y_(2)-y_(1))/(x_(2)-x_(1))`

=
`(10-5)/(2+2)`

=
`(5)/(4)`

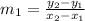
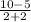
Let the slope of the tangent which is perpendicular to this line is '
`m_(2)`'

Then by the property of perpendicular lines,

`m_(1)* m_(2)=-1`

`(5)/(4)* m_(2)=-1`

`m_(2)=-(4)/(5)`

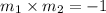
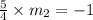
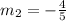
Now the equation of the line passing though (2, 10) having slope
`m_(2)=-(4)/(5)`

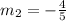
y - y' =
`m_(2)(x-x')`

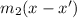
y - 10 =
`-(4)/(5)(x-2)`

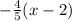
y - 10 =
`-(4)/(5)x+(8)/(5)`

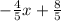
y =
`-(4)/(5)x+(8)/(5)+10`

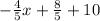
y =
`-(4)/(5)x+(58)/(5)`

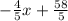
Therefore, equation of the line will be, y =
`-(4)/(5)x+(58)/(5)`