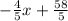Answer:
a). Center of the circle = (-2, 5)
b). Equation of the line ⇒ y =
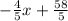
Explanation:
Equation of the circle is,
x² + 4x + y²- 10y + 20 = 30
a). [x² + 2(2)x + 4 - 4] + [y²- 2(5)y + 25] - 25 + 20 = 30
[x² + 2(2)x + 4] - 4 + [y² - 2(5)y + 25] - 25 + 20 = 30
(x + 2)² + (y - 5)²- 29 + 20 = 30
(x + 2)² + (y - 5)²- 9 = 30
(x + 2)² + (y - 5)² = 39
By comparing this equation with the standard equation of a circle,
Center of the circle is (-2, 5).
b). A point (2, 10) lies on this circle.
Slope of the line joining this point to the center (-2, 5),
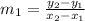
=
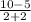
=
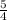
Let the slope of the tangent which is perpendicular to this line is '
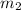 '
'
Then by the property of perpendicular lines,
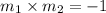
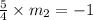
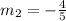
Now the equation of the line passing though (2, 10) having slope
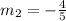
y - y' =
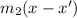
y - 10 =
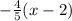
y - 10 =
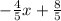
y =
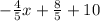
y =
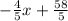
Therefore, equation of the line will be, y =