Question

cubical tank 1 meter on each edge is filled with water at 20 degrees C. A cubical pure copper block 0.46 meters on each edge with an initial temperature of 100 degrees C is quickly submerged in the water, causing an amount of water equal to the volume of the smaller cube to spill from the tank. An insulated cover is placed on the tank. The tank is adiabatic. Estimate the equilibrium temperature of the system (block + water). Be sure to state all applicable assumptions.

Answer 1

final temperature = 26.5°

Step-by-step explanation:

Initial volume of water is 1 x 1 x 1 = 1
`m^(3)`

Initial temperature of water = 20° C

Density of water = 1000 kg/
`m^(3)`

volume of copper block = 0.46 x 0.46 x 0.46 = 0.097
`m^(3)`

Initial temperature of copper block = 100° C

Density of copper = 8960 kg/
`m^(3)`

Final volume of water = 1 - 0.097 = 0.903
`m^(3)`

Assumptions:

• since tank is adiabatic, there's no heat gain or loss through the walls
• the tank is perfectly full, leaving no room for cooling air
• total heat energy within the tank will be the summation of the heat energy of the copper and the water remaining in the tank.

mass of water remaining in the tank will be density x volume = 1000 x 0.903 = 903 kg

specific heat capacity of water c = 4186 J/K-kg

heat content of water left Hw = mcT = 903 x 4186 x 20 = 75.59 Mega-joules

mass of copper will be density x volume = 8960 x 0.097 = 869.12 kg

specific heat capacity of copper is 385 J/K-kg

heat content of copper Hc = mcT = 869.12 x 385 x 100 = 33.46 Mega-joules

total heat in the system = 75.59 + 33.46 = 109.05 Mega-joules

this heat will be distributed in the entire system

heat energy of water within the system = mcT

where T is the final temperature

= 903 x 4186 x T = 3779958T

for copper, heat will be

mcT = 869.12 x 385 = 334611.2T

these component heats will sum up to the final heat of the system, i.e

3779958T + 334611.2T = 109.05 x
`10^(6)`

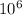
4114569.2T = 109.05 x
`10^(6)`

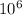
final temperature T = (109.05 x
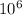`10^(6)`)/4114569.2 = 26.5°