Answer:
A .

B.
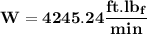
C. The system is at steady state but not at equilibrium
Step-by-step explanation:
Given that:
The volumetric flow rate of the water = 15 gallons per minute
The diameter of the pipe that leaves the pump is 1 inch.
A. The objective here is to determine how much work flow is done by the water as it leaves the pump and enters the pipe
The work flow that is said to be done can be expressed by the relation :
W = P × V
where;
P = pressure
V = volume
Also the given outlet pressure is the gauge pressure
The pressure in the pump P is can now be expressed by the relation:
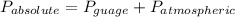
 = 10 psig + 14.7 psig
= 10 psig + 14.7 psig
 = 24.7 psig
= 24.7 psig
W = P × V
W = 24.7 psig × 15 gal/min
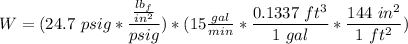

Thus ; the rate of flow of work is said to be done by the water at

B.
Given that :
The water returns to the pool through an opening that is 1.5 inches in diameter.
where the pressure is 1 atm.
Then ; the rate of work done by the water as it leaves the pipe and enter the pool is as follows:
W = P × V
W = 1 atm × 15 gal/min
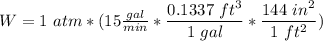
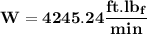
Thus ; the rate of flow of work done by the water leaving the pipe and enters into the pool is at
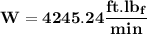
C.
We can consider the system to be at steady state due to the fact that; the data given for the flow rate and pressure doesn't reflect upon the change in time in the space between the pump and the pool.
On the other-hand the integral factor why the system is not at equilibrium is that :
the pressure leaving the pipe is different from that of the water at the surface of the pool as stated in the question.