Question

True or False


1. A solution to 8 = -x + 10 is 2

Answer 1

Hey ! there

Answer:

• True

Explanation:

In this question we are given with an equation that is 8 = -x + 10 and we have also given its solution that is 2 .And We are asked to tell whether the solution of given equation is true or false .

For finding that we must have to solve the equation .

Solution : -

`\longrightarrow \qquad \: 8 = -x + 10`

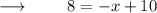
Step 1 : Flipping the equation so that there's ease in solving :

`\longrightarrow \qquad \: - x + 10 = 8`

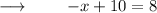
Step 2 : Subtracting with 10 on both sides :

`\longrightarrow \qquad \: - x + \cancel{10 }- \cancel{ 10} =8 - 10`

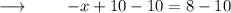
On further calculations , We get :

`\longrightarrow \qquad \: - x = - 2`

Step 3 : Multiplying with -1 on both sides :

`\longrightarrow \qquad \: - x * - 1 = - 2 * - 1`

We get :

`\longrightarrow \qquad \: \blue{\underline{\boxed{ \frak{x = 2}}}}`

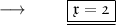
• Therefore , it's TRUE that 2 is the solution of given equation .

Alternative Solution : -

There's another easy way to check whether 2 is solution of given equation or not . This is done by substituting value of x that is 2 in given equation that is 8 = -x + 10 . So substituting value of x ( solution ) in given equation :

• 8 = - ( 2 ) + 10

• 8 = -2 + 10

• 8 = 8

• L.H.S = R.H.S

As we can see that left side is equal to right side .

• Therefore , it's TRUE that 2 is the solution of given equation .

#Keep Learning

Answer 2

• True

Explanation:

So, Lets find out if the solution is true or not, So first let us find the value of x.

⇒ 8 = -x + 10

We can rewrite the equation as,

⇒ -x + 10 = 8

Subtracting 10 from both sides we get :

⇒ -x + 10 – 10 = 8 – 10

⇒ -x = -2

Multiplying both sides by (-1) :

⇒ -1(-x) = -1(-2)

⇒ x = 2

Therefore,

• The statement "A solution to 8 = -x + 10 is 2" is true