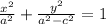Question

QI - The sum of the distance of a moving

point from the points (c,0) and (-c,0) is
always 2a units. Find the equation to the locus
of the moving point.​

Answer 1

`(x^2)/(a^2)+(y^2)/(a^2-c^2)=1`

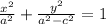
Explanation:

Let P be the moving point and the given points be A (c,0) and B (-c, 0). If (h, k) be the co-ordinates of any position of P on its locus then:

PA + PB = 2a

PA = 2a - PB

PA² = 4a² + PB² – 4a ∙ PB

PA² – PB² = 4a² – 4a ∙ PB

[(h - c)² +(k - 0)²] - [(h + c)² +(k - 0)²] = 4a² – 4a. PB

-4hc = 4a² – 4a∙PB

a ∙ PB = a² + hc

Taking square

a² ∙ PB² = (a² + hc)²

a² [(h + c)² + (k - 0)²] = (a² + hc)²

a² [h² + c² + 2hc + k²] = a⁴ + 2a²hc + h²c²

a²h² – h²c² + a²k² = a⁴ – a²c²

(a² – c²)h² + a²k² = a² (a² – c²)

h²/a² + k²/(a² – c²) = 1

Therefore, the required equation to the locus of P is

`(x^2)/(a^2)+(y^2)/(a^2-c^2)=1`