Answer:
Neither expression satisfies the given rational root.
Explanation:
To find the right answer, we just need to replace the given root in each expression and see which one gives zero.
First expression.
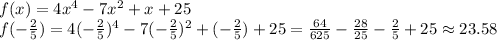
Second expression.
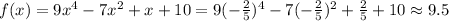
Third expression.
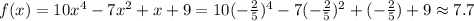
Fourth expression.
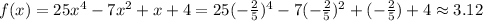
Therefore, neither expression satisfies the given rational root.