Question

A player tosses a die 6 times.If gets a number 6 Atleast two times he wins 2 dollars ,otherwise he looses 1 dollar.. Find the expectation of the amount if he wins

Answer 1

Expected value = -0.2101

Step-by-step explanation :

Givena discrete variable the expected value is given as:

E(x) = xp(x) + yp(y)

Where x and y are the values the variables can assume, and p(x) and p(y) are their respective probabilities.

Probability that a player gets 6 at least twice = p(x ≥ 2) = 1 - p(x≤ 2)

= 1 - p(0) - p(1)

But p(0) = 0.3349

p(1) = 0.4018

p(x ≥ 2) = 1 - 0.3349 - 0.4018

= 0.2633

p(y) = 1 - p(x)

= 1 - 0.2633

= 0.7367

Expected value = 2(0.2633) + (-1)(0.7367)

= -0.2101

A loss of $0.2101 is expected.

Answer 2

`E(x)=-0.2101`

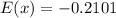
Explanation:

The expected value for a discrete variable is calculated as:

`E(x)=x_1*p(x_1)+x_2*p(x_2)`

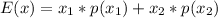
Where
`x_1` and
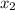`x_2` are the values that the variable can take and
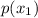`p(x_1)` and
`p(x_2)` are their respective probabilities.

So, a player can win 2 dollars or looses 1 dollar, it means that
`x_1` is equal to 2 and
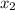`x_2` is equal to -1.

Then, we need to calculated the probability that the player win 2 dollars and the probability that the player loses 1 dollar.

If there are n identical and independent events with a probability p of success and a probability (1-p) of fail, the probability that a events from the n are success are equal to:

`P(a)=nCa*p^a*(1-p)^(n-a)`

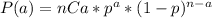
Where
`nCa=(n!)/(a!(n-a)!)`

So, in this case, n is number of times that the player tosses a die and p is the probability to get a 6. n is equal to 6 and p is equal to 1/6.

Therefore, the probability
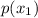`p(x_1)` that a player get at least two times number 6, is calculated as:

`p(x_1)=P(x\geq2)=1-P(0)-P(1) \\\\P(0) =6C0*(1/6)^(0)*(5/6)^(6)=0.3349\\P(1)=6C1*(1/6)^(1)*(5/6)^(5)=0.4018\\\\p(x_1)=1-0.3349-0.4018\\p(x_1)=0.2633`

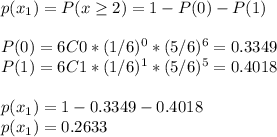
On the other hand, the probability
`p(x_2)` that a player don't get at least two times number 6, is calculated as:

`p(x_2)=1-p(x_1)=1-0.2633=0.7367`

Finally, the expected value of the amount that the player wins is:

`E(x)=x_1*p(x_1)+x_2*p(x_2)\\E(x)=2*(0.2633)+ (-1)*0.7367\\E(x)=-0.2101`

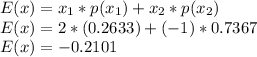
It means that he can expect to loses 0.2101 dollars.