Answer:
The flagpole 12 meters tall
Explanation:
Running from the top of a flagpole to a hook in the ground there is a rope that is 13 meters long
∵ The hook is 5 meters from the flag pole
∵ The flagpole and the ground ⊥ to each other
By using Pythagoras theorem:
hypothenus side is 13m
base is 5m
how tall is the flagpole is x
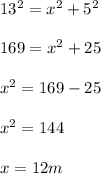
The flagpole 12 meters tall